![]()
.
In general, people working with mathematics on the web want three things:
These three needs are complex and not yet completely satisfied because:
So, we need:
Currently, following the W3C recommended procedures, a user can do the following:
The advantages are:
and the bonus side-effect,
It should be noted that stylesheets can be used to 'chunk' mathematical expressions. An example of how this might be done is provided by the expression that follows:
The formula makes it possible to predict the result with accuracy.
compared with:
The formula [insert formula here] makes it possible to predict the result with accuracy.
Using stylesheets to determine what is visible/available at any time, may facilitate the reading of a mathematical argument or text and indirectly benefit novices and experts: the novices by saving them the distraction of the full text on each reading, and the expert who does not need to be given the detail of the text. Such chunking could be achieved simply by the use of appropriate stylesheets. In such a case, the same paper may be capable of presentation in several forms ranging from a 'fast, first reading format' to a 'precise, detailed, formal mathematical format'.
Scalable Vector Graphics (SVG) also allows for chunking, but particularly of graphical representations. In the context of structured images, with sub-elements, this means that many images can be made fairly accessible to people with vision disabilities.
Whereas mathematical concepts are represented in symbolic notation, geometricians do not use symbolic notation so much as 2D and 3D images and discussion of them in relatively standard 'text' formats. In recent years. the teaching of geometry has been revolutionised by the use of computer technologies.
Experts use geometry to represent complex problems and find ways to work on the problems using the constraints and freedoms of geometry. Students of geometry using Cabri Geometre, and Geometer's Sketchpad, and similar application packages, experience geometry as a language of constraints and freedoms. Students, using the computer applications, see how under the constraints of construction generalisations (such as the triangle characteristic of a space) may be maintained even though other objects in the construction change in size. Making geometry physically accessible through the movement of a computer mouse, for example dragging a point of the edge of a circle and so increasing the size of the circle, is one example of where equivalent alternative sensory experiences can be used by all students. All students, including those with sight disabilities, can feel the flexibility but the problem is to represent the effects. Application packages can provide alternative, equivalent representations, as do Cabri and Geometers' Sketchpad.
In other contexts, mathematics students have benefited from differential geometric worlds and the decentralised 'object oriented' worlds of geometry made possible by Logo and *Logo. These applications have had millions of users 'doing' mathematics, building their own mathematical worlds. In these environments, the emphasis is on programming as a way of representing mathematics but the outcome can in many forms, including tactile, aural, visual and even physical objects moving in space. Students with disabilities have been able to work in these environments.
In "Speaking of Mathematics" by Brian Hayes (March, 1996), http://www.amsci.org/amsci/issues/Comsci96/compsci96-03.html,
Brian Hayes explains that the fundamental problems with mathematics come from:
- the fact that it uses primarily a written language and it does not 'read' in a linear fashion, and
- computers add characters to screens in a linear way, and again this is not generally suitable for mathematical expressions.
The equation above was created using symbols that are both written and pronounced symbol by symbol in a linear way from left to right. It was converted into a graphic and is displayed on graphical browsers but has no alternative representation. Users who cannot see the graphic have no idea what is on the screen.
Including adequate ALT text would allow screen readers to provide an equivalent rendering of the expression. Typical ALT text for the above graphic is:
ALT="A cubed plus B cubed equals the quantity A plus B times the quantity A squared minus A,B plus B squared" and inserted with the image into the web page.
When a sighted person reads mathematics to a blind person, a standard way of reading the mathematics has to be negotiated between the reader and the listener. For an excellent description of this process, see http://www.rit.edu/~easi/easisem/talkmath.htm. In a situation where this cannot be done in real time, a standardised way of reading the expression will be required.
One part solution to the problem is to provide a reading (text) in a 'long description', linked to the image and text by having a 'd' following the image. It might say one or more of the following:
But there will most probably still be difficulties for some users.
Alternatively, a mathematical expression may be provided in standard text (ascii) format with special formatting, as follows:
a3+b3=(a+b)(a2-ab+b2)
Without formatting, this appears as a3+b3=(a+b)(a2-ab+b2). The correct meaning of the expression is contained in a mixture of the characters and the formatting. So text alone is not adequate for mathematical expressions and many expressions cannot be written as easily in text as this example.
It is not normal practice for web users to need to see the formatting instructions and in the case of screen readers, they are best ignored in most situations. This is not the case for mathematical expressions. One solution is to have the text formatting styled in ways that make it available, for instance, to those using screen readers. This might mean having superscript characters rendered in a higher pitch than others, or to have changes from normal to super to sub script identified by some other sound.
Mathematical Mark-up (MathML from W3C at http://www.w3.org/Math/) is an XML mark-up language for mathematical notation. MathML has been written with universal accessibility as a priority. It offers two formats for representing an expression: presentational tags and semantic/content tags. Users can write expressions in a accessibility compliant editor and view or access the symbolic representations on the web with an accessibility and mathML standards-compliant user agent.
Usually this requires a MathML enabled web editor such as Amaya, or a mathematics application - see the W3C lists of MathML compliant browsers and the list of MathML compliant mathematical software.
An older but currently recommended solution is to use the application that TV Raman developed (called AsTeR after his seeing-eye dog).
In "Speaking of Mathematics" by Brian Hayes (March, 1996), there is a good explanation of what has become the most common solution to the mathematics problem. See http://www.amsci.org/amsci/issues/Comsci96/compsci96-03.html
Mathematicians and others usually talk together about mathematics employing blackboards, whiteboards, or showing or writing on overhead slides. Currently, where mathematics is to be communicated using computers, or to be done with computer assistance, the most widely adopted solution is to use the Tex formatting language, or its more highly developed derivative, LaTex, often with the assistance of mathematics symbolic manipulation applications.
Given an equation such as:
![]() (audio),
TeX linearizes the two-dimensional layout of the equation.
(audio),
TeX linearizes the two-dimensional layout of the equation.
Here is the LaTeX encoding of the equation given above:
$$\lim_{x \to \infty}\int_0^x e^{-y^2}\dy = \frac{\sqrt{\pi}}{2}$$
As Hayes explains:
"Terms that begin with a backslash are "control sequences," most of which are easy to figure out. For instance, the sequence \infty generates the infinity sign, \int is the integral sign, and \frac makes a fraction out of the two groups of symbols that follow it. The underscore and caret (_ and ^) designate subscripts and superscripts respectively. Of course no one would want to read mathematics in this form, but raw TeX is not meant for human consumption. It is processed by a computer program that renders it in a more palatable form on a display screen or on the printed page.
AsTeR(Audio System for Technical Readings) is also a computer program that accepts TeX notation as input and produces a rendering as output, but the rendering is audible rather than visual. The program does not simply read out the TeX code literally; a rendering that began "dollar dollar backslash lim underscore left-bracket x ..." would be incomprehensible. What is needed is an approximation to the oral rendering that would be given by a mathematically knowledgeable human reader, perhaps something like: "The limit, as x goes to infinity, of the integral, from y equals zero to x, of e to the minus y squared, dy, equals the square root of pi, over 2." (I have had a hard time punctuating this sentence, because of the unusual pattern of pauses that readers employ to indicate the grouping of mathematical expressions. Perhaps this difficulty is another sign of the tenuous connection between written and spoken mathematics.)"
There is a comprehensive demonstration of Aster available on the web (see http://www.cs.cornell.edu/Info/People/raman/aster/aster-toplevel.html) and papers about it and its use.
"AsTeR has three main components. A recognizer parses Latex notation and creates an internal representation that is easier for the program to manipulate. An audio formatting language, called AFL, renders the parsed text using both speech and nonspeech sounds. The third component is a facility for audio browsing, or actively traversing the structure of a document."
Because mathematical expressions are not always legible from left to right, AsTeR has to read the whole expression before starting to speak it out, often with a pause for making it sensible in the audio rendition. The spoken version includes auditory clues such as when superscripts or subscripts are being spoken. Finally, the control of the audio has to be given back to the user so they, like their counter-parts who view the expression, can move backwards and forwards reconsidering particular elements of the expression.
So mathematical expressions can be accessible to the blind. The problem is that they must be prepared with care, and often this means using software that produces Latex or Tex.
As most users reading mathematical expressions are at some stage likely to want to use the mathematics, images of mathematics are not recommended. For writers of mathematics for the web
For users of mathematics on the web, demand that:
If mathematics on the web is marked up properly in MathML, it may be possible to use it directly by buying a mathematical symbolic editor that understands MathML and is itself accessible. There is a comprehensive list of these available at http://www.w3.org/Math/
An example of mathematics working on the web, initially via an applet, and then mathML, is available at http://www.math.pitt.edu/~gartside/math0450/chaos/
(Please note that this resource was written in 2002 and there are now other solutions to some of the problems. In particular, please see the material on making math accessible at the Design Science website: http://www.dessci.com/en/solutions/access/ - note added 6/2/2007)
This is an older solution from Dave Raggett (http://www.w3.org/People/Raggett/EzMath/ or local) that is being brought up to date.
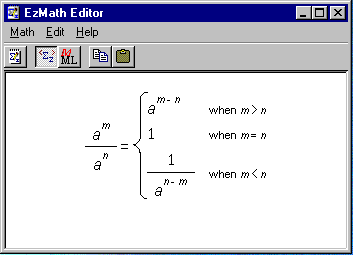
"The Web lacks an effective means for embedding mathematical expressions in Web pages. Hitherto, authors have been forced to use bitmapped images, which are slow to load, complex to produce, and look bad when printed.
EzMath provides an easy to learn notation for embedding mathematical expressions in Web pages. The notation is inspired by how expressions are spoken aloud together with a few abbreviations for conciseness (e.g. x^y denotes x raised to the power y).
EzMath covers a widely used subset of mathematics. EzMath focusses on the meaning of mathematical notation rather than just how it looks on paper (or screen). The EzMath editor makes it very easy to create the markup for pasting into your web pages, either in the EzMath notation or as MathML."
Recently Dave Raggett has said:
"I have been working in a complete re-implementation of EzMath in C++ which will very soon become an open source project on Source Forge. The goal is to get other people to help with its development and its integration into other tools. Several people have already approached me with offers of help...
The new EzMath code base will allow a variety of uses such as the ability to convert XHTML+EzMath to:
- XHTML+MathML
- XHTML+images
- XHTML+ActiveX controls
- XHTML+Netscape plug-ins
When converting to MathML, the EzMath expression is retained as the value of <math> alttext attribute. This documents the MathML in a human intelligible way, but can also be edited and used to regenerate the MathML automatically, thereby offering an easy means to edit MathML content."
Se http://www.software.ibm.com/techexplorer/
This software allows users to create active mathematics that can be inserted into web pages or Powerpoint. (In PowerPoint, insert the techexplorer ActiveX control in the presentation via the Control Toolbox dialog. The inserted techexplorer content can itself contain commands that send the mathematical expressions to a mathematics application, like Mathematica (use the \evalLink control sequence to connect a techexplorer document to the Mathematica Add-in).)
IBM's site boasts:
"IBM techexplorer is a plug-in for Navigator and Internet Explorer, an IE 5.5 XML Behavior, and an ActiveX control for applications like Microsoft PowerPoint and Word. techexplorer enables the display of TeX, LaTeX and MathML documents and the publishing of interactive scientific material on the Web. Version 3.1 includes full support for MathML 2.0, augmented LaTeX display, new ways to enliven documents via scripting/programming and a web equation editor. New to 3.1 is a Macintosh version, Mathematica connectivity, IE MathML Behavior and a 30-day trial Professional Edition."
The Wolfram website (http://www.wolfram.com/news/techexplorer.html) explains:
"The widespread use of HTML has revolutionized communications, but HTML itself has limitations. Before MathML, the only way to publish any but the simplest formulas on the web was to transmit them as bitmapped images, an inefficent and awkward workaround. The MathML format allows for the web transmission of mathematical expressions in a much more efficient way. Mathematica 4 can already save notebook documents as HTML/MathML with one simple command, but most users could not take full advantage of this capability since the most popular browsers do not include built-in support for the MathML extension.
techexplorer fills this gap by allowing the most popular browsers to render expressions transmitted in either TeX format (a popular format for technical documents in academia) or MathML format. The upcoming release of Mathematica 4.1 will include the techexplorer format in its list of "Save As Special..." options, letting users save their notebooks into a techexplorer-savvy form."
and continues:
Figure 1 A Mathematica notebook
Figure 2 The same notebook saved as a techexplorer document and displayed in a browser
"However, the connection between techexplorer and Mathematica does not end there. techexplorer is primarily a display technology, but thanks to a special software interface developed by IBM and Wolfram Research, techexplorer will be able to use Mathematica's kernel to evaluate expressions and formulas directly from the browser (Windows only). Moreover, users can paste MathML expressions directly into their Mathematica notebooks, and Mathematica will interpret them properly--making cut-and-paste from the web as easy for mathematical formulas as it is for text."
MathML is the mark-up standard recommended by W3C. It has been developed with accessibility in mind and is currently being further developed so that its accessibility features will be available to those who need them. MathML provides for two equivalent representations for every mathematical expression: a semantic representation and a syntactical, or symbolic one.
The following example shows how MathML works.
The equation
x2 + 4x + 4 =0
is represented in two ways; first using presentational tags, then using semantic tags. The presentational tags generally start with "m" and then use "o" for operator "i" for identifier "n" for number, and so on. The "mrow" tags indicate organization into horizontal groups.
<mrow>
<mrow>
<msup> <mi>x</MI> <mn>2</mn> </msup> <mo>+</MO>
<mrow>
<mn>4</mn>
<MO>⁢</MO>
<MI>x</MI>
</mrow>
<MO>+</MO>
<mn>4</mn>
</mrow>
<MO>=</MO>
<mn>0</mn>
</mrow>
The semantic tags take into account such concepts as "times", "power of" and so on:
<apply>
<plus/>
<apply>
<power/>
<ci>x</CI>
<cn>2</cn>
</apply>
<apply>
<times/>
<cn>4</cn>
<CI>x</CI>
</apply>
<cn>4</cn>
</apply>
MathML encoding can be used on pages encoded in XHTML. See how to put MathML into a web page that is written in XHTML. The pages can be viewed using most graphical browsers with a plug-in or directly with browsers such as Amaya.
"MathML permits one to write math so that it is rigorously defined, but it also permits "presentation" markup - i.e. one can represent x squared as x to power 2, which is rigorous, or as x superscript 2, which is ambiguous. Math computational programs generally have inference rules so x superscript 2 will invariably be interpreted as x squared, but other visual formatting conventions aren't so clear." (John Gardiner, private communication.)
The final step involves providing stylesheets to make mathematics expressions audible - audio style sheets written in XSL. ATRC is working with IBM to develop some aural stylesheets that will make mathematical expressions marked in MathML accessible. This is an ongoing project but two examples (http://nide.snow.utoronto.ca/MathML/gauss.wav) and (http://nide.snow.utoronto.ca/MathML/gauss2.wav) are already available from the site at http://nide.snow.utoronto.ca/MathML/mathstrat.html This approach may be very useful to mathematics students in general, as it will help make mathematical expressions more meaningful for many who find them difficult to read.
Validating MathML - test suites http://www.w3.org/Math/testsuite - validator http://www.w3.org/Math/validator
from W3C site...
"The XHTML namespace may be used with other XML namespaces as per [XMLNAMES], although such documents are not strictly conforming XHTML 1.0 documents as defined above. Future work by W3C will address ways to specify conformance for documents involving multiple namespaces.
The following example shows the way in which XHTML 1.0 could be used in conjunction with the MathML Recommendation:
<html xmlns="http://www.w3.org/1999/xhtml" xml:lang="en" lang="en"> <head> <title>A Math Example</title> </head> <body> <p>The following is MathML markup:</p> <math xmlns="http://www.w3.org/1998/Math/MathML"> <apply> <log/> <logbase> <cn> 3 </cn> </logbase> <CI> x </CI> </apply> </math> </body> </html>The following example shows the way in which XHTML 1.0 markup could be incorporated into another XML namespace:
<?xml version="1.0" encoding="UTF-8"?> <!-- initially, the default namespace is "books" --> <book xmlns='urn:loc.gov:books' xmlns:isbn='urn:ISBN:0-395-36341-6' xml:lang="en" lang="en"> <title>Cheaper by the Dozen</title> <isbn:number>1568491379</isbn:number> <notes> <!-- make HTML the default namespace for a hypertext commentary --> <p xmlns='http://www.w3.org/1999/xhtml'> This is also available <a href="http://www.w3.org/">online</a>. </p> </notes> </book>"
See a description from a user's perspective with excellent advice about how to work with MathML: http://arts.bev.net/roperldavid/mathinternet.htm.
"MathML authoring tools are becoming available rapidly. Mozilla can display mathML as a native code (not certain whether it can today, but it will soon). And I believe IBM Tech Explorer will work with Netscape in Macs and Unix. I know it works with IE in Windows. Lethargy is the only thing that is keeping people back from using mathML on the web. Nobody wants to learn a new ap, particularly brand new ones that aren't always bug-free or extremely user-friendly. And of course mathML is not yet accessible. Should be within a year or two or three."
(See http://www.mozilla.org/projects/mathml/ (local))
So, until there are stylesheets that render the mathML accessible (see above), there is no gain - or is there?
"MathML is a good markup language because it was designed by a small but able committee representing the needs of the community mathML would serve. MathML is the only example I know of a committee-designed solution that turns out to be better than any single person is likely ever to derive.
Math markup has been a controversial issue for several decades. The publishing industry insisted on a language that required no knowledge of math so that an uneducated monkey could typeset math. The mathematics community wanted a semantic language so the expressions were rigorous. mathML had to be both, so the committee made the sensible (in my opinion) decision to provide both alternatives. Accessibility of presentation was incorporated as well as the committee could conceive by including lots of layout possibilities that could be included into a style language.
Major members of the mathML community were the companies doing computational math, so I will assure you that the needs of that community were included. As were the needs of publishers. They did as good a job as possible without benefit of a crystal ball to include needs of future expansion. Until I begin using mathML heavily I cannot comment on deficiencies. However at present it seems almost perfect."
W3C has published a report (http://www.w3.org/Math/iandi/ or local) on the known implementation activities of MathML 1 and relates their experience to the criteria which were set out as the requirements of the Candidate Review period for MathML 2.
Christopher Weaver reports (http://lists.w3.org/Archives/Public/www-math/2000May/0055.html or local):
"One of the difficulties that developers of accessibility software face is the inability to recognise the logical structures that are required to accurately render the material acording to the rules of a particular accessible medium. This is painfully true in regard to North American braille mathematics (Nemeth Code). In addition to the logical elements of text structure one has to worry about the logical elements of mathematical expressions. Sadly, most current texts and web documents do not present mathematics in a usable, logically structures manner.
However, MathML 2.0 is a step in the right direction, If Texts were marked up up with MathML this burden would be greatly reduced. The presentation markup is exquisitely explicit in it structuring of most mathematical expressions. In fact, All post secondary mathematics that is marked up in XHTML1.0 and MathML2.0 can be automatically transcribed, provided that there is a standard representation of all glyphs used in the text (Non-standard glyphs require a transcriber's interpretation)."
Note received 18/7/2001:
Hello Liddy,
Most of Maple 7's functionality is accessible to visually impaired users who utilize either speech- or Braille-synthesizing screen readers, such as the JAWS screen reader. According to Dr. Peter Torpey, a blind physicist at Xerox who uses JAWS at work, Maple's interface is quite legible to screen readers, with only a few exceptions. There are some user-interface features that have not yet been optimized for accessibility to screen readers, but we will be addressing these in our next product release sometime in 2002. I will be happy to provide you with more details if you like.
Maple software does not generate any sound outputs, so hearing impaired users will have the same accessibility as users with normal hearing.
Please let me know if I can be of further assistance in your preparation of specifications for students with special needs.
Best regards,
Jason Schattman, Ph.D.
Manager, Applications Marketing
Waterloo Maple Inc.
57 Erb St. West
Waterloo, Ontario N2L 6C2
(519) 747-1278 x 351
http://www.mapleapps.com
There are problems for authoring tool developers, including people who make templates for others to use. MathML is not yet widely used and not native to commonly used browsers, and many of the courseware packages that were sold in the past were not acccessibility-aware. This is, to a large extent, changing but it is still unlikely that in the short term, courseware developers will be able to adapt fast enough to make the problem 'go away'. In the meantime, tool makers can help their users solve the problem by presenting best practice information and, where possible, incorporating software that supports good mathematics mark-up.
It is worth visiting http://www.mathmlconference.org/Talks/rudisill/ to see about using mathematics notation in WebCT. The authors in that case wrote the mathematics notation in Word using the Equation Editor and then translated it into MathML using WebEQ generator - a shareware translator - and users viewed the notation with their graphical browsers augmented with the WebEQ plug-in (free). - from W3C at http://www.w3.org/Math/
There are a number of ways in which mathematics is currently made available to blind and other students with special needs. Such practices are, in general, able to be used in conjunction with the web. The following section refers to some of these practices. In many cases, the applications and devices considered are used to support students doing mathematics.
A MathML document could use SVG for both laying out equations and drawing graphs of those equations. In examples below, we show how to describe SVG components and their relationships by embedding RDF metadata and SMIL markup in the SVG - see http://www.w3.org/TR/SVG-access/.
see http://dots.physics.orst.edu/agc.html
This a self-voicing Windows application that has been under development and testing for some time by the Science Access Project at Orgeon State University. It includes the capabilities to:
In a 1999 CSUN paper by Thomas A. Ley, there is a description of a Braille calculator that can do standard maths and also can be used to generate tactile graphs (http://www.dinf.org/csun_99/session0113.html).
"Blazie Engineering is the leading designer of portable, note taking computers for the blind and visually impaired in the world. The versatile product line is anchored by the popular Braille 'n Speak 2000 (TM). The line includes models for speech only users, Braille only users, users preferring to type, users preferring to Braille, or users preferring a combination of any of the above.
Braille 'n Speak is right at home in the classroom, and its sturdy design and dependability have stood the test of time. Exceptional battery life, simple command structure and portability make it perfect for students of any age, but the question remains, how can a Braille 'n Speak (TM) help in math class? Blazie Engineering presents a four tiered approach to meeting the needs of math students who are blind and visually impaired. Each unit includes a built-in basic calculator as well as a fully functioning scientific calculator.
Additional software is available for students needing the power of a financial calculator. Finally, graphing calculator functionality is available for the blind using Graphit in conjunction with any Braille embosser. "
Last updated: 8 March 2002